Non-linear structures
Tree
- A tree is a data structure that stores elements in a hierarchy.
- The elements are referred as nodes, and the lines connect them are edges. Each node has a value or an object.
- The top node in a tree is called root, and the nodes have no children are leaf nodes.
Binary Trees
- Use cases:
- Represent hierarchical data
- Databases indexing
- Autocompletion
- Compilers
- Compression (JPEG, MP3)
- Binary search tree
- All value in the left sub-tree is less than the value of current node
- Achieve logarithmic time complexity, each comparison throw away half of the items
- Operations: O(log(n)) better performance than array and linked list
- Lookup
- Insert (first lookup then add link)
- Delete (first lookup then remove it by reconnecting the edges)
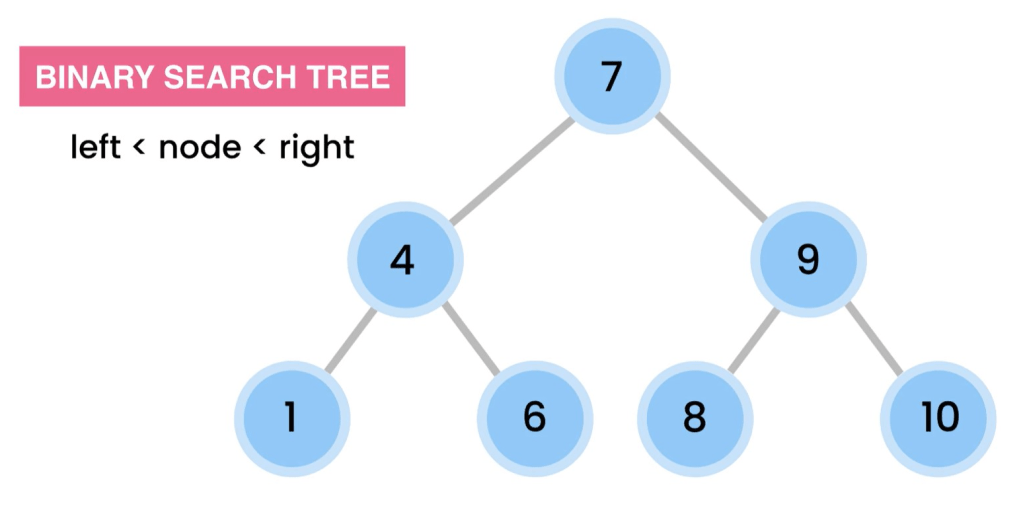
- Traversing
- Breadth first (level order traversal): visit the nodes at the same level before visiting the nodes on the next level [7, 4, 9, 1, 6, 8, 10]
- Depth first
- Pre-order: root, left, right [7, 4, 1, 6, 9, 8, 10]
- in-order: left, root, right [1, 4, 6, 7, 8, 9, 10 ] -> result is in ascending order
- post-order: left, right, root [1, 6, 4, 8, 10, 9, 7] -> leaf nodes visited first

- Recursion
- A approach for implementing repetition in our code without loop
- Happens when a function calls itself
- Base condition: the condition to terminate the recursion
- Depth and height of a node
- depth: the number of edges from root to the node
- height: is the opposite of depth, the number of edges along the longest path to a leaf (post order traversal)
- Minimum value in a tree
- Binary tree: recursively find the minimum value of the small trees O(n)
- Binary search tree: the left most leaf O(log(n))
- Exercises:
- Validating a binary tree
- Nodes at K Distance
- getAncestors()
AVL Trees
- A balanced tree: height(left) – height(right) <= 1
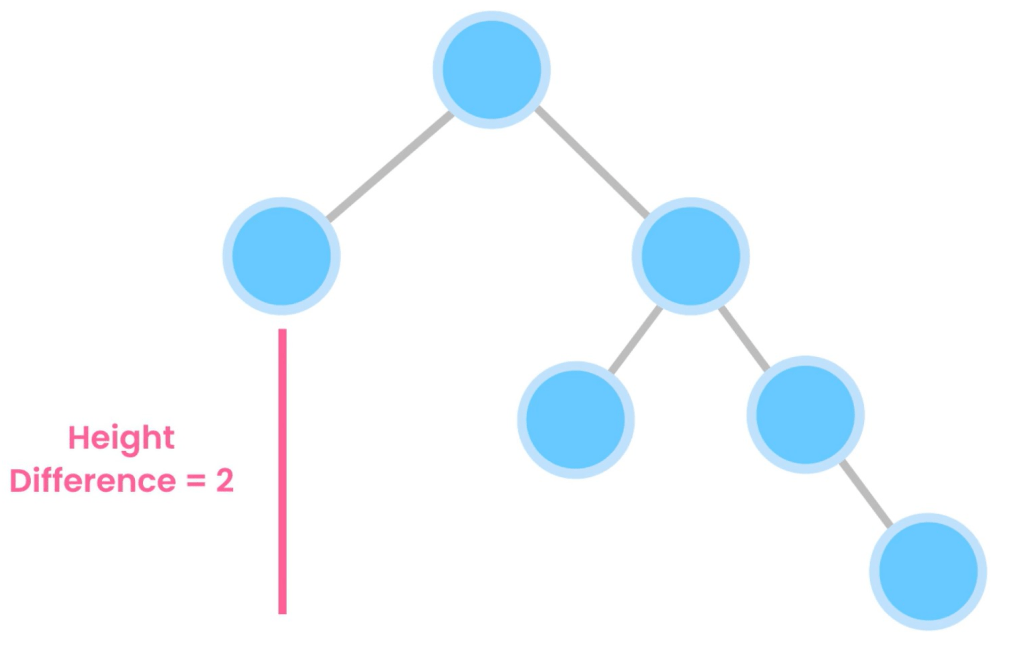
- When the inserted values are in sorted order
- Self-balancing tree: AVL tree (Adelson-Velsky and Landis)
- automatically rebalance themselves every time add or remove nodes, using rotations
- Rotations: which method to use depends which side of the tree is heavy
- Left (LL): when the tree is heavy at the right, put weight on left to push down (add edge)
- Right (RR)
- Left-Right (LR): the imbalance is from left child, right sub tree (smallest number in middle)
- Right-Left (RL) (largest number in middle)
- BalanceFactor = height(L) – height(R)
- > 1 => left heavy
- < -1 => right heavy
- Implementing rotation
- after rotation, the height of root and new root would change, reset height
- the root is changed, insert function instead of having no return type, should return new root node
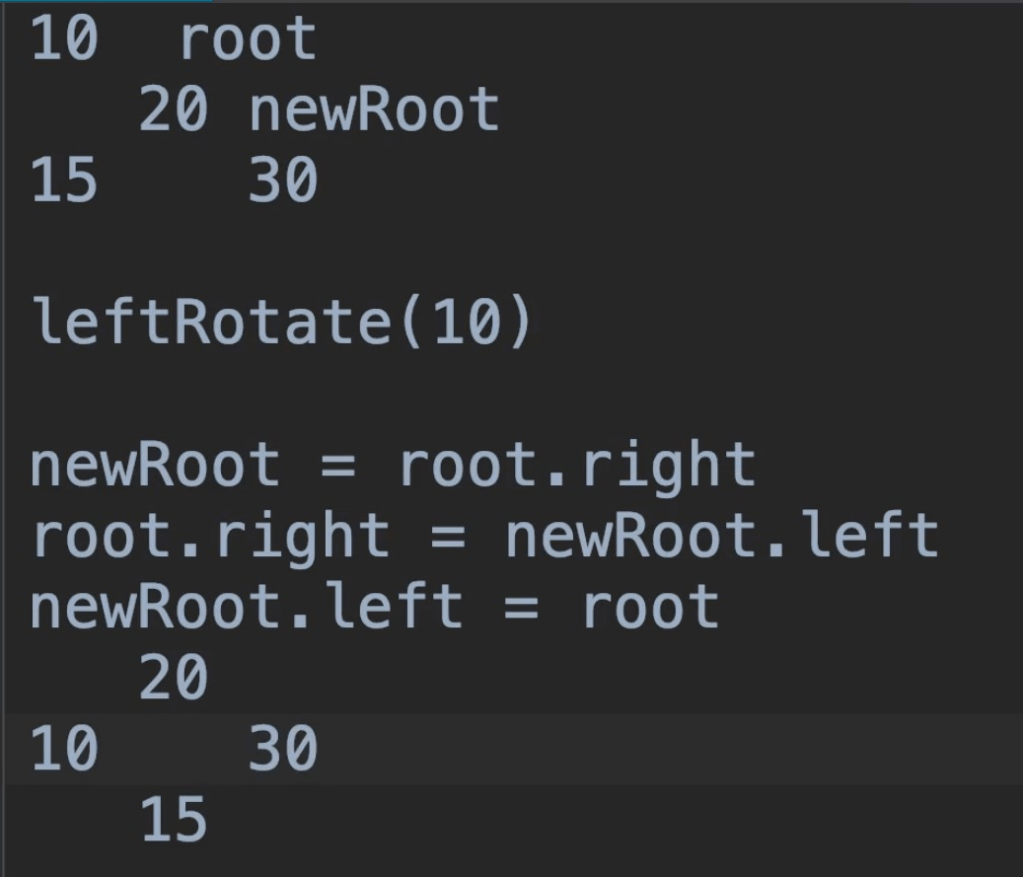
- Exercises:
- check a perfect tree: the relation between height and size
- BST:
- Average: O(log(n)): each time remove half
- Worst O(n): like a linked list
Heaps
- Requirement for heap
- Complete tree: each level except the last level is completely filled, and the last level is filled from left to the right.
- Heap property: every node is larger or equal to its children
- Use cases:
- Sorting (HeapSort)
- Graph algorithms (shortest path)
- Priority queues
- Finding the Kth smallest / largest value
- Heaps are always stored in array
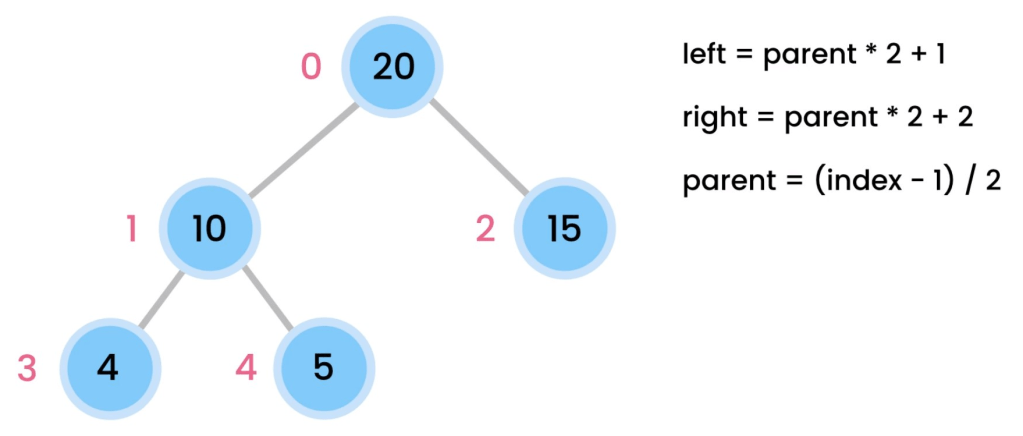
- Insert(): add to the end in the array, compare with its parent value, if it’s larger, bubble up until the right position O(log(n))
- remove(): move the last item to the root, compare with its chidren, if it’s smaller, bubble down until the right position O(log(n))
- Sorting data:
- Priority Queue: implementation with heap, insert O(n) -> O(log(n)), delete O(1) -> O(log(n))
- Exercise:
- Heapify: transforming an array into a heap.
- Actually don’t have to perform the operation on the leaf nodes, because they have no children. And the number of leaf nodes is half of the array size.
- The last parent node: (n / 2 ) – 1
- Heapify: transforming an array into a heap.

Tries
- Operations: O(L), L is the length of the word searching for / inserting / deleting
- Lookup
- Insert
- Delete
- Build a trie
- start with root, which is always empty
- at the end of the inserting word, mark it as the end of a word

- When using array to store the children node, it’s kind of waste of memory, optionally could use hash table <key, Node>
- Traversals
- Pre-order: visit the root first
- Post-order: visit the leaf first
- Exercise:
- remove a word: post-order
- auto completion: pre-order
Graphs
- Types:
- directed graph (twitter)
- undirected graph (facebook)
- edges may also have weight (find shortest path between two nodes)
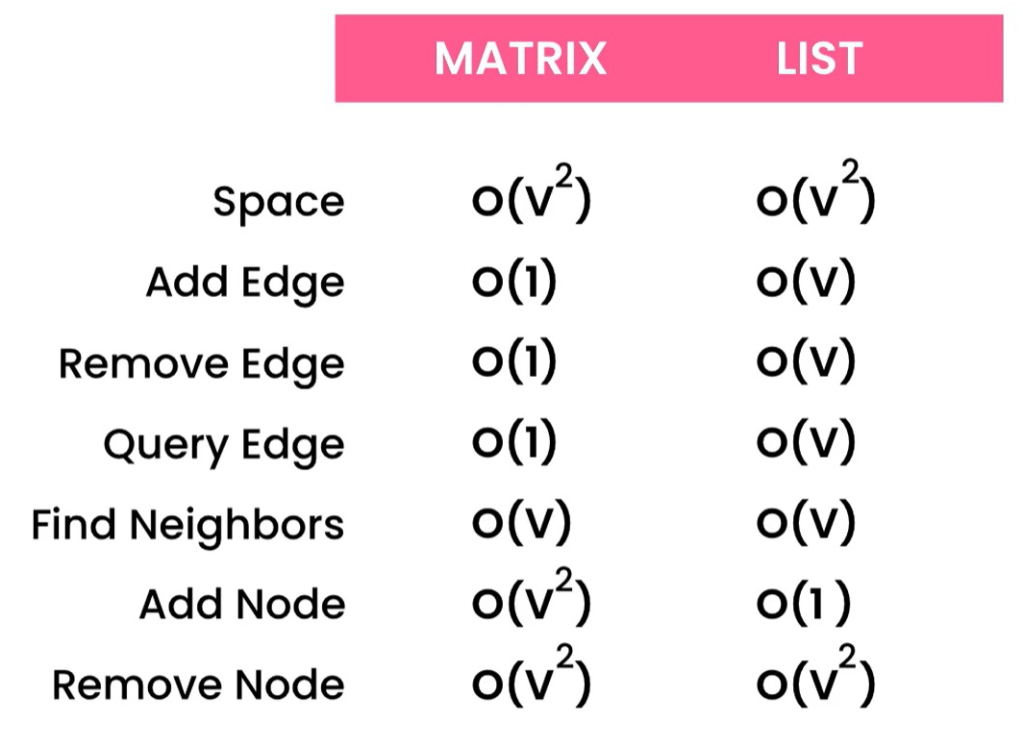
- Adjacency matrix

- Adjacency matrix Operations:
- space O(v²) v = number of vertices
- Add / remove / query edge: O(1), use hash table to store nodes and their indexes
- Find neighbors : O(v)
- Add / Remove node: O(v²), copy and move to new matrix
- Adjacent List: array of linked lists, the linked list contains adjacent nodes, only store the edges that exist
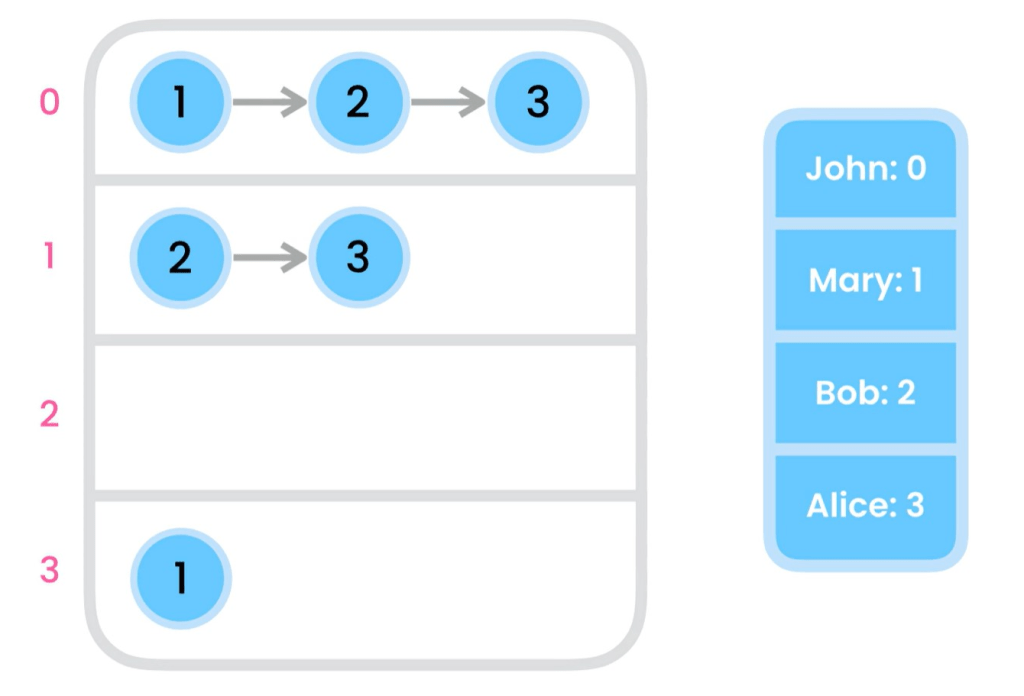
- Dense graph: each node connected to all the other nodes
- E = V * (V – 1)
- Operations:
- Space complexity: O(V + E) = O(V + V² -V) = O(V²)
- Add node: O(1)
- Remove node: O(V + E) = O(V²)
- Add edge: O(K) (K is the number of the neighbors ), worst case: O(V) (multi graph, two nodes can be connected by multiple edges: O(1))
- Remove edge: O(K), worst case: O(V)
- Query edge: O(K), worst case: O(V)
- Comparison
- When is a dense graph, matrix has a better performance
- Implementation
- One hash table for the nodes Map(String, Node)
- one hash table for the edges (adjacencyList) Map<Node, List<Node>>
- add nodes and edges: add node to the nodes list and adjacencyList
- remove nodes and edges: remove all the connections, remove from adjacencyList, remove from nodes list

- Traverse:
- Depth-first:
- A Set to track visited node
- Stack
- Breadth-first:
- Queue
- Depth-first:
- Topological Sorting
- may have different result
- work with directed acyclic graph (without cycle)
- Detect cycle in a directed graph
Undirected Graphs
- Weighted graph
- Dijkstra’s shortest path algorithm
- Cycle detection:
- Visiting nodes & visited nodes
- spanning tree: E = V – 1
- Minimum Spanning tree:
- Prim’s Algorithm: extend the tree by adding the smallest connected edge
- Minimum Spanning tree: